For the past couple of weeks in class we have been focusing on the volume of solid shapes. In class, we have used plastic solid shapes and have filled them with water, and measured out the water to see how much volume certain solid shapes have, such as rectangular prisms and spheres. For daily work this week I decided to measure my own solid shapes using two different methods. One being measuring the shapes and finding volume with an equation and the other method I will use is measuring volume by putting the shapes in water.
Fortunately, my mom is an AP Biology and Environmental Science teacher so she supplied me with the graduated cylinders, marbles, and some rocks. Also I am fortunate that my parents never gave away my old building blocks from when I was younger so I can use them for my math lesson.
Fortunately, my mom is an AP Biology and Environmental Science teacher so she supplied me with the graduated cylinders, marbles, and some rocks. Also I am fortunate that my parents never gave away my old building blocks from when I was younger so I can use them for my math lesson.
The first activity I did used the building blocks. I measured the volume of rectangular prisms, triangular prisms, cylinders, and a cube. The way I found the volume was by measuring with a ruler and then using an equation. This method for finding volume would be good for students grades 6-8.
The first shapes I measured were the big rectangular prism and the smaller rectangular prism. The equation to find the volume of a rectangular prism is...
length x width x height
So, I measured the sides of the prisms. The larger prism had a length of 11.5 cm, a width of 5.5 cm, and a height of 2.4 cm. So, 11.5 x 5.5 x 2.4= 149.16 centimeters cubed.
The smaller rectangular prism had a length of 5.3 cm, a width of 3.4 cm, and a height of 2 cm. So, 5.3 x 3.4 x 2= 36.04 centimeters cubed.
length x width x height
So, I measured the sides of the prisms. The larger prism had a length of 11.5 cm, a width of 5.5 cm, and a height of 2.4 cm. So, 11.5 x 5.5 x 2.4= 149.16 centimeters cubed.
The smaller rectangular prism had a length of 5.3 cm, a width of 3.4 cm, and a height of 2 cm. So, 5.3 x 3.4 x 2= 36.04 centimeters cubed.
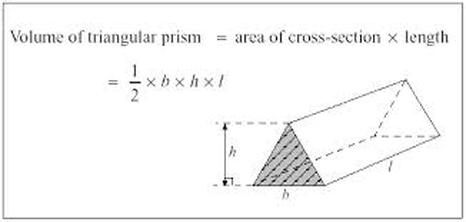
The next shapes I measured were the little green triangular prism and the bigger red triangular prism. The equation for finding the volume of a triangular prism is...
1/2 x Base x Height x Length.
Here is a diagram that I found on Google Images that might be helpful for when you find the volume of a triangular prism:
1/2 x Base x Height x Length.
Here is a diagram that I found on Google Images that might be helpful for when you find the volume of a triangular prism:
After measuring the smaller triangular prism the base was 2.5 cm, the height was 3.5 cm, and the length was 8 cm. So, 1/2 x 2.5 x 3.5 x 8= 35 cm cubed.
The larger triangular prism had a base of 2.6 cm, a height of 3 cm, and a length of 11.5 cm. So, 1/2 x 2.6 x 11.5 x 3= 44.85 centimeters cubed.
The larger triangular prism had a base of 2.6 cm, a height of 3 cm, and a length of 11.5 cm. So, 1/2 x 2.6 x 11.5 x 3= 44.85 centimeters cubed.
Then I measured the two cylinders. To find the volume of the cylinders I took
pi (3.14) x radius squared x height.
So I measured the bigger cylinder first the radius was 1.5 cm and the height was 10 cm. So I then I did (1.5)^2 x 10 x Pi= 70.69 cm cubed.
The smaller cylinder had a radius of 1.4 cm and a height of 3.9 cm. So, (1.4)^2 x 3.9 x Pi= 24.01 cm cubed.
pi (3.14) x radius squared x height.
So I measured the bigger cylinder first the radius was 1.5 cm and the height was 10 cm. So I then I did (1.5)^2 x 10 x Pi= 70.69 cm cubed.
The smaller cylinder had a radius of 1.4 cm and a height of 3.9 cm. So, (1.4)^2 x 3.9 x Pi= 24.01 cm cubed.
Finally, I saved the easiest for last. Finding the volume of the cube. Each side had a side length of 5 cm so I knew I had to do 5 x 5 x 5 since 5 cm was the length, height, and width. My answer was 125 cm cubed.
This volume activity led me into finding the volume of irregular solid shapes. I decided to find the volume of a marble, a granite rock, and a quartz mineral.
This volume activity led me into finding the volume of irregular solid shapes. I decided to find the volume of a marble, a granite rock, and a quartz mineral.
To find the volume of each of these objects I filled the graduated cylinder to 40 ml with water. Then I dropped each object in the graduated cylinder filled with water. Then however much the water increased when I dropped the object in the water is the volume of the object.
The first object I measured was the marble. I dropped it in and the water filled up to 42 ml. So, 42-40= 2. So the volume of the marble is 2 ml or 2 cm cubed.
The second object I measured was the quartz mineral. I dropped it in the water and the water increased to 44 ml, so 44-40= 4 ml or 4 cm cubed.
Then the last object I dropped into the graduated cylinder was the granite rock. When I dropped it in the cylinder the water increased to 43 ml so 43-40= 3 ml or 3 cm cubed.
I think this activity would be good for upper elementary school students since there is no complicated equations involved and this activity is more visual. All the students have to do is be able to measure out water and subtract numbers. It's necessary to have objects that will sink to the bottom of the graduated cylinder or measuring cup, because the activity will not work with items that float.
The first object I measured was the marble. I dropped it in and the water filled up to 42 ml. So, 42-40= 2. So the volume of the marble is 2 ml or 2 cm cubed.
The second object I measured was the quartz mineral. I dropped it in the water and the water increased to 44 ml, so 44-40= 4 ml or 4 cm cubed.
Then the last object I dropped into the graduated cylinder was the granite rock. When I dropped it in the cylinder the water increased to 43 ml so 43-40= 3 ml or 3 cm cubed.
I think this activity would be good for upper elementary school students since there is no complicated equations involved and this activity is more visual. All the students have to do is be able to measure out water and subtract numbers. It's necessary to have objects that will sink to the bottom of the graduated cylinder or measuring cup, because the activity will not work with items that float.
Reflection: I think these two volume activities I did would be good for students to visually understand volume and they get to work hands on with measuring tools, instead of doing book work problems and just having to visualize the solid objects in their minds.
Feedback: Would these activities benefit students knowledge of volume? What other ways could I teach volume besides the ways we've done in class and the two ways I just did?
Feedback: Would these activities benefit students knowledge of volume? What other ways could I teach volume besides the ways we've done in class and the two ways I just did?


 RSS Feed
RSS Feed