This week I decided to complete the pattern's worksheet on braille and codes. I also read the article "Patterns at Your Fingertips" by Daniel J. Brahier. I decided to do this as my weekly work because it made me realize math can help people who are in need, such as the blind. These worksheets and article really demonstrates how math can relate to the real world.

The first worksheet I completed was "Pixel Patterns". The first thing the worksheet asked me to do was create a six pixel font and make 26 letters in the boxes. Each pixels had to have a different design. I then had to write my first name with the code.
This is what I came up with:
After I created my own code, I was asked what problems I had with my font and what some good things were about my font. I said that a problem could be that some of the letter combinations are similar and it could get confusing, I also said the font could be difficult to memorize. Some good things I pointed out about my font was that it was original and all of the letters were different from each other (which was the goal).

The next thing the worksheet asked me to do was to think of my font mathematically. It asked me how many different combination possibilities are with 1 pixel? 2 pixels? and then 3 pixels? With one pixel there are only two combinations, with two pixels I discovered there are only 4 possible combinations, and with three pixels I discovered there were 8 possible combinations.
Do you see a numerical pattern yet?
I discovered quickly that each time the number of pixel's goes up, the number of possibilities doubles.
Example: 2 pixels has 4 combinations and 3 pixels has 8 combinations, so 4+4=8
So then I was asked what the next pixel's arrangements were. Using math I found that 4 pixel's had 16 possible combinations, 5 pixels had 32 combinations, and 6 pixel's had 64 combinations.
I found all of these answers just by doubling the number of possibilities each time.
Ex: 8+8= 16 so there are 16 possible combinations in the 4 pixels
16+16=32 so there are 32 possible combinations with the 5 pixels
32+32= 64 there are 64 combinations with the 6 pixels
The next thing I was asked honestly made me think. The worksheet asked if it matters if the tiles are arranged. My solution to that question was that it does not matter how the tiles are arranged. I double checked my answer by sketching out the different tile arrangement and comparing it to the original tile arrangement

These problems all led up to the actual braille alphabet. The first pattern I noticed in the braille alphabet was that the first row of letters (a-j) only has dots in the first two rows. The second pattern I noticed was that the second row of letters (k-t) had dots in all three of the rows, but in the third row there was only a dot in the first column. The last pattern I noticed was that the third row of letters (u-z) had dots in all three of the rows, but had dots in both the first and second column of the third row (with the exception of w).
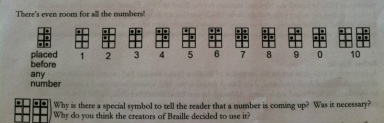
Braille numbers were the last thing the worksheet pointed out. Notice, that numbers are the same as letters, the only thing that differentiates them is the braille symbol that notifies the reader that they are about to be reading numbers instead of letters. This special symbol is very important, because it prevents confusion among the reader. Without this symbol the reader would assume they are reading letters.
This worksheet prepared me for the article "Patterns at Your Fingertips" by Daniel J. Brahier. The article starts off with a very great idea. Combining literature with math. They suggested that the students read a book about Helen Keller before they begin to do the math activities. I thought this was a wonderful idea, because this shows how math can help people, such as the blind. Without math, there would not be Braille, and without Braille, blind people would not be able to read. This shows how much of an impact math makes on people's lives.
I also noted in the article, "Barbier, a former soldier, showed Louis how soldiers had used a complicated twelve-dot system to communicate top-secret information on the battlefield" (Brahier 522). This soldier inspired Louis Braille to create the braille alphabet. This excerpt also shows that math even had an impact on the military because of these mathematical codes, these soldiers were able to communicate on the battlefield.
Now getting to the actual lesson plan for 2nd and 3rd graders, I thought this article used a great activity to teach kids how to make different codes and patterns. Using four of one color and four of another it has kids create different combinations of color patterns.

I tried out the activity using the colors red and green and came up with the solution that there are 8 possible color pattern combinations for a "3-tile train"
The activity then told me to find how many color combinations there were with 4 tiles. I quickly discovered that the result was going to end up like the first worksheet. The color combinations just doubled, so there were 16 different color combinations.
Ultimately the whole activity was like the first worksheet I completed, but it was more 2nd and 3rd grade friendly. Using colors made this activity more exciting and I believe it would help them learn the concept better.
The last thing discussed in the 2-3 grade activity was that these codes can be used to solve math problems. For example: "Each child in class has 3 pencils. If there are 15 children, how many pencils are there altogether?" Then there are two different answers, "Our answer" and "Our answer in braille"
I think this is a good idea, because it gives the kids more to think about. Rather than just a simple, "what is 15x3?" Instead this activity encourages them to find the answer and then find the braille pattern that goes with the answer.
The article also explains the same activity for 4th-6th graders. Ultimately the activity is the same, but more advanced. The article has them fill out the table that I filled out in the first worksheet I completed, and then asks them to answer a problem similar to the question in the 2nd to 3rd grade activity, but more advanced.
Reflection: I think this braille activity is a great way for kids to learn how to apply their math skills and knowledge to real life. It is also good for them to see that math is very helpful in the world and greatly has helped out the blind. This activity also will take problem solving and creating patterns to another level. All around this is a very helpful, eye-opening activity.
Sources:
Brahier, Daniel J. "Patterns at Your Fingertips." Web. 7 Sept. 2013.




















 RSS Feed
RSS Feed