For the past couple of weeks in class we have been focusing on the volume of solid shapes. In class, we have used plastic solid shapes and have filled them with water, and measured out the water to see how much volume certain solid shapes have, such as rectangular prisms and spheres. For daily work this week I decided to measure my own solid shapes using two different methods. One being measuring the shapes and finding volume with an equation and the other method I will use is measuring volume by putting the shapes in water.
Fortunately, my mom is an AP Biology and Environmental Science teacher so she supplied me with the graduated cylinders, marbles, and some rocks. Also I am fortunate that my parents never gave away my old building blocks from when I was younger so I can use them for my math lesson. The first activity I did used the building blocks. I measured the volume of rectangular prisms, triangular prisms, cylinders, and a cube. The way I found the volume was by measuring with a ruler and then using an equation. This method for finding volume would be good for students grades 6-8. The first shapes I measured were the big rectangular prism and the smaller rectangular prism. The equation to find the volume of a rectangular prism is...
length x width x height
So, I measured the sides of the prisms. The larger prism had a length of 11.5 cm, a width of 5.5 cm, and a height of 2.4 cm. So, 11.5 x 5.5 x 2.4= 149.16 centimeters cubed.
The smaller rectangular prism had a length of 5.3 cm, a width of 3.4 cm, and a height of 2 cm. So, 5.3 x 3.4 x 2= 36.04 centimeters cubed. The next shapes I measured were the little green triangular prism and the bigger red triangular prism. The equation for finding the volume of a triangular prism is...
1/2 x Base x Height x Length.
Here is a diagram that I found on Google Images that might be helpful for when you find the volume of a triangular prism: After measuring the smaller triangular prism the base was 2.5 cm, the height was 3.5 cm, and the length was 8 cm. So, 1/2 x 2.5 x 3.5 x 8= 35 cm cubed.
The larger triangular prism had a base of 2.6 cm, a height of 3 cm, and a length of 11.5 cm. So, 1/2 x 2.6 x 11.5 x 3= 44.85 centimeters cubed. Then I measured the two cylinders. To find the volume of the cylinders I took
pi (3.14) x radius squared x height.
So I measured the bigger cylinder first the radius was 1.5 cm and the height was 10 cm. So I then I did (1.5)^2 x 10 x Pi= 70.69 cm cubed.
The smaller cylinder had a radius of 1.4 cm and a height of 3.9 cm. So, (1.4)^2 x 3.9 x Pi= 24.01 cm cubed. Finally, I saved the easiest for last. Finding the volume of the cube. Each side had a side length of 5 cm so I knew I had to do 5 x 5 x 5 since 5 cm was the length, height, and width. My answer was 125 cm cubed.
This volume activity led me into finding the volume of irregular solid shapes. I decided to find the volume of a marble, a granite rock, and a quartz mineral. To find the volume of each of these objects I filled the graduated cylinder to 40 ml with water. Then I dropped each object in the graduated cylinder filled with water. Then however much the water increased when I dropped the object in the water is the volume of the object.
The first object I measured was the marble. I dropped it in and the water filled up to 42 ml. So, 42-40= 2. So the volume of the marble is 2 ml or 2 cm cubed.
The second object I measured was the quartz mineral. I dropped it in the water and the water increased to 44 ml, so 44-40= 4 ml or 4 cm cubed.
Then the last object I dropped into the graduated cylinder was the granite rock. When I dropped it in the cylinder the water increased to 43 ml so 43-40= 3 ml or 3 cm cubed.
I think this activity would be good for upper elementary school students since there is no complicated equations involved and this activity is more visual. All the students have to do is be able to measure out water and subtract numbers. It's necessary to have objects that will sink to the bottom of the graduated cylinder or measuring cup, because the activity will not work with items that float. Reflection: I think these two volume activities I did would be good for students to visually understand volume and they get to work hands on with measuring tools, instead of doing book work problems and just having to visualize the solid objects in their minds.
Feedback: Would these activities benefit students knowledge of volume? What other ways could I teach volume besides the ways we've done in class and the two ways I just did?
Today, our Math 221 class attended Dr. Kevin Cloninger's lecture, "Thinking Outside the Job: Helping Students Learn to Live the Good Life". For daily work we were asked to write on our blog a response/summary of the lecture we attended.
Summary:
Going into this lecture I had no idea what to expect. I thought it was going to be a lecture just on how to be a better teacher. This lecture did inform me on how to be a better teacher, but it also informed me how to live a better life. Cloninger started the lecture off with talking about well-being and what it is. When I think of well-being I immediately think health, but otherwise I do not think very much about it. Cloninger began discussing that children and adults are not necessarily living a good life. Several children and adults are affected by childhood obesity and other diseases caused by poor eating habits and lack of exercise. Cloninger also brought up that depression will soon be the leading illness/disability. What Cloninger was getting at was the fact that in the 21st century we as human beings are not focusing on having a "good life". The things we are teaching our students and children are that the most important things in life are a good job and having a lot of money. Cloninger reminded us that this is definitely not true.
Cloninger expressed that we need to focus on having a good life instead of having a good job. There are several problems occurring in the world right now, such as hunger and climate change. We need to focus on fixing our ways of life to be healthy and live in a healthy world. Something Cloninger kept saying was that "It's too late to be pessimistic". We need to start making changes in our lives now.
Another thing that Cloninger discussed was how reliant the world is on technology. The fact that people are constantly using our phones, going on the internet for things such as Facebook, and watching television. Cloninger had some data of how many hours people waste their lives using technology like this.
Overall, he was saying as educators and parents we need to focus on students and children's well-being, instead of focusing on the global economy. It's necessary to focus on a good life to successfully live in the 21st century.
My Response: I thought it was strange because I had been thinking a lot about the things Cloninger was saying in his lecture before I even attended his lecture. I thought I was the only one thinking these thoughts, but luckily I am not.
I think teaching students how to live a good life is essential. We also need to teach kids and even teach ourselves to live in a 21st century world. We really need to focus on climate change, since ultimately human's are destroying the world. We also need to focus on our health and eating habits, since human's are also destroying themselves with very unhealthy eating habits.
As far as technology goes, I feel we rely on it way too often. Recently I have tried to "boycott" Facebook (except for when I have to post my math weekly works on Facebook) and I have been trying to use unnecessary technology less often. My reason for boycotting Facebook has been due to my recent research on Facebook and depression. Honestly, there is so much I could say about these subjects and I could write pages and pages about the issues of the 21st century, so I will try to stop ranting and get back to my response.
Overall, I feel that as a future teacher we really need to focus on well-being and teaching kids how to be healthy and live in a healthy world. I definitely am trying to start living a healthy lifestyle myself, and I want to promote living a healthy lifestyle to future generations. I believe this lecture was very beneficial for our class to attend and I hope other people benefited as much as I did from it.
Family Math Night finally approached this past Thursday night at a Grand Haven elementary school. The game I had prepared for the students was a probability game called, "Build an Animal". When my partner and I tested the game out on the 5th graders before family math night the game was a great success. The 5th graders loved it and thought it would be a great game for younger students. The experience with the 5th graders made me confident about Family Math Night.The night of Family Math Night I had prepared all of the animals for my game and created a rule sheet. When the night started my partner and I had to wait a little bit for anyone to come play our game. Finally, the first students wandered into our room and we explained the game. One of the students was very young, possibly in kindergarten while her brother was probably in about 2nd grade. The age difference between the two players really affected the game play. The younger student did not understand some of the rules and decided to do her own thing and just roll the die and choose whatever animal part she wanted, while her older brother tried to follow the rules. That was something I was very unprepared for. Children not following the rules of the game was a common pattern throughout the night. Younger students would get very upset when they rolled a number of a part they already had and so they had to skip a turn. They also were upset when they rolled a 5 which meant they had to steal a part from another player. We quickly had to adapt the rules for the younger students so that when they rolled a number they already had, they could roll again. With the stealing, we eventually changed the rule to, "steal a part from any pile" to avoid catastrophe.
Another problem we faced at Family Math Night was explaining the math behind our game to younger students. The students that were probably in 1st grade and under struggled understanding the game, let alone the math behind it. Before Family Math Night I thought that younger children could easily play the game, but after actually working with them, I realized it was difficult for them. This made me realize this game is definitely meant for students from 2nd grade to possibly 4th grade.
Family Math Night taught me that I need various adaptations of a game for each age group when working at an event like this. Though, there were some drawbacks of our game on the actual night, some students really enjoyed our game. The students that enjoyed our game the most were probably in the 2nd-4th grade range. Overall, Family Math Night was a great experience and has taught me a lot about teaching and I feel that it has made me a better teacher.
Family Math Night is this Thursday and we cannot believe how fast it is approaching! Our activity is called "Build an Animal" and it is a math game based on probability. In my last post about Family Math Night I roughly explained the basis of the game and some of the game rules. In my last post I was preparing to play this game with the Grand Haven 5th Graders for the first time. Now, after playing the game with several different kids, they gave Sara and I excellent feedback. Some feedback was brutally honest, but as a whole the feedback we got helped us out in the long run. Questions/Feedback Received from the 5th Graders: "What math is in this game/what is probability?""There should be more animals to choose from""There should be a paper with all of the different rules and which each number on the die represents" Things Learned from 5th Graders Playing the Game:- We need a fair way to decide who goes first.
- We need to explain what probability is before we start the game and we need to possibly keep track of what the probability is after each turn (for more advanced/higher grade level students)
- We need more dice so there can be more players.
- More animals are needed, for more choices and more fun.
- To prevent fighting possibly have kids choose an animal part from a bag so it is random and fair. We could have the kids figure out the probability of getting their favorite animal.
New and Improved Game:
Before the Game:
Before the game begins and is explained Sara & I are planning on explaining what probability is. We might hand out a handout on what probability is if needed. Then we will go on to explaining the game.
Explanation of the Game: There will be four piles or bags with different animal parts. The different piles consist of tails, legs, bodies, and heads. The goal of the game is to create a complete animal with four legs, one tail, a body, and one head. The animal can be as crazy as the student wants. Each student will have a die and will take turns rolling a die. The number the student rolls represents a different rule/body part. Whoever is the first to complete an animal wins the game.
To decide who gets to go first, Sara & I decided to have all of the players roll their dice and whoever rolled the highest number went first.

Something we previously added to the game was a list of the rules for each number on the die to help guide the students as they play the game.

Another thing added to the game was three more animals for more variety and more players.
Unfortunately, I was not able to test out the game in Grand Haven a second time with these new additions, I was not able to receive more feedback from the 5th graders. To get the best test experience I could I played the game with my friend, Tony. The first time I won the game and the second time Tony won. The game went smoothly and no big catastrophes happened. Reflection: Making this Family Math Night activity took a lot of time and work with creating the different animal parts. The feedback from the fifth graders definitely helped the process. The activity is pretty much completed, but there are some finishing touches that need to be done.
Feedback: Throughout this project I feel like I/we have been struggling with making this activity vividly have math. Is explaining probability before the game enough? Or should we have the students record the probability of winning the game after each turn? I feel like doing that would be difficult for the younger children and would make the game less fun, but I'm not sure.
Finding the area can be very simple and other times it can be very difficult and frustrating. Shapes that are easy to find the area of are regular shapes. I classify regular shapes a rectangle, square, triangle, pentagon, etc... For these shapes, you can easily put them on grid paper and count the boxes that exist within them. To get more technical, for some of these you can use an equation to find the area of these shapes such as:
Rectangle & Square: Base x Height
Triangle: 1/2 x Base x Height
Using a Geoboard I made a couple of regular shapes and found the area of them.
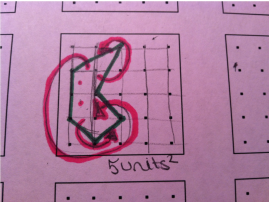
 Finding area of a rectangle: Since I know that to find area I need to do base x height I measured with the Geoboard the side lengths. The height of the rectangle is 1 and the base of the rectangle is 4. So, 4 x 1 = 4, so the area of this rectangle is 4 units squared.
 Finding area of a triangle: Now that we know the equation to find the area of a triangle is 1/2 x Base x Height I now know to measure the base and height of the triangle I made on the Geoboard. The base of this triangle is 2. The height of this triangle is 3. So now I go back to the formula, 1/2 x 2 x 3 = 3
If you wanted to count of the squares in the triangle that is possible as well, you just need to mix and match the squares that have been split. I created lines with rubber bands on the Geoboard to represent grid paper so that it would help with adding up the squares. My result of an area was still 3 units squared.
Now, I am going to get into the shapes that are more difficult to find the area of which I refer to as,irregular shapes. With irregular shapes it is more difficult to find the area by counting up the squares inside of them. So, in order to find the area of these shapes I usually split the irregular shape into different sections and work from there.
Here are some examples of irregular shapes:  I also decided to make some irregular shapes on a Geoboard and work out what the area was. I started with the shape to the left.
I decided to actually figure out the area of this shape on a piece of paper that had a Geoboard sketch on it to make things easier. I drew grid lines behind the shape to help me:
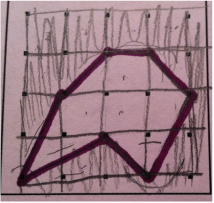
 For this shape I decided to count the squares within the shape to find the area. I had to do some matching and estimating to come up with my answer. The crazy pink arrows show the pieces of square that I matched together to make 1 square unit. In the end I decided the area was approximately 5 units squared.
 To the left is the second shape I created to find the area of. Once again I put this shape on Geoboard paper to make finding the area easier.
 To find the area of this shape, instead of counting the squares inside the shape I decided to count the squares that were outside of the shape. Total, there are 16 squares that make up a Geoboard. When I counted the squares outside of the shape I counted that there were approximately 9 squares outside of the shape. Then I subtracted that number from 16 so, 16-9=7. From this I found that the shape had an area of approximately 7 units squared. To check, I also counted the squares on the inside. When doing this I came up with an area of 6.5 units squared. Either way I believe both methods work, but since I randomly made these shapes I'm not sure what the precise answer is. So using both of the answers I got I would say the shape had an area of around 7 units squared.
Reflection: Ever since area was introduced to me in elementary school I've always found finding the area of an irregular shape difficult. I always feel like there should be an equation for everything, but that's just how I've learned how math should be. Now doing this as a college student I find that it's okay to make mistakes and get a wrong answer. Doing these area problems it is hard to get an exact answer on your own and I feel that working together on these problems help. I also learned that there are several different ways to look at these problems and different ways to solve for the area. Everyone has different perspectives.
Feedback: What area did you receive for these shapes? What method did you use to find the area? Is there just one correct way to find area of a shape?
With Family Math Night approaching in less than a month all of my Math 221 time has been spent thinking about what needs to be prepared for Family Math Night. Our class will be working with 5th graders of Grand Haven to make this night happen. This week I spent most of my time figuring out ideas/games I can present to the 5th graders when our class meets with them on Wednesday. Over the past week I have looked through several math games, trying to find a fun and mathematical game. I looked at the Family Math Night Starter Ideas Google Doc to help come up with an idea. The game that stood out to me the most on the Google Doc was the, "Build an Animal" game. What made me look at this game when first glancing through the page was the fact that it was using animals with math. I personally love animals and I know that most children also love animals. So that led me to look further into the game. How to play, "Build an Animal": To play this game you need a die with each different number on the die representing a different animal body part. (Such as 1 being a body, 2 being a head...etc.) Whatever number the student rolls they will look at what animal body part the number represents and take that part from the pile. The student will keep rolling the die until they get all of the body parts to build a complete animal. This game will also be a race to see who can make a whole animal the fastest.
Math in "Build an Animal": The math behind this game is all about probability. When the student rolls a die there are 6 different possibilities that the student will roll. The probability is 1/6 or 16%. On the website, "Math is Fun" I found a good equation of probability:
Probability of an event happening = Number of ways it can happen/Total Number of outcomesThings to do for preparation: My partner and I need to cut out different animal parts and decided what numbers represent what body part and if we want one number to represent something else such as, "Take a part from another player". We also need to decide what makes an animal a "complete" animal. In general we need to figure out what we want the exact rules of the game to be. Reflection: Preparing for Family Math Night is showing me what it takes to be teacher and the work that is needed for making lesson plans or games. This activity is teaching me how to teach others math and I'm sure after the actual event I will have improved my math teaching skills. Feedback: Do you have any advice to make this game better? Any rules that should be added? Sources: Math is Fun: http://www.mathsisfun.com/data/probability.htmlFamily Math Night Google Doc: https://docs.google.com/document/d/18XQOUnBqavQHaFOL7b9CDPrmW7NegY9ZgwFB7N1kMLo/edit
In class on Friday we worked with Oreo cookies. We worked with Single Stuf Oreo's, Double Stuf Oreo's, and Mega Stuf Oreo's. Our goal was to find out if Double Stuf Oreo's and Mega Stuf Oreo's really had more "stuf" than a Single Stuf Oreo. Is Double Stuf really double stuffed? What does mega stuffed mean? We had so many unsolved Oreo mysteries at the beginning of class.
To solve these Oreo mysteries our class had each person individually measure different things. First we measured the weight in grams of a whole Single Stuf Oreo, Double Stuf Oreo, and a Mega Stuf Oreo. We also weighed the different cookies without the stuf in the middle and then we also weighed only the stuf in the middle of each Oreo. We also measured the height of each different type of Oreo as a whole cookie, just the stuf, and then one side of the individual cookie. The last thing we measured was the diameter of the cookie and then we measured the diameter of the white stuf of each different Oreo.
Once we found all of the measurements for the Oreo's we then added our data to a Google Document. This now leads to my weekly work. Using all of the information from the Google Document I decided to analyze the Oreo data by finding the Mean, Median, Mode, and Range of our data. I decided to only use the data for the stuf in the middle of the cookie because that is what we really care about, right?
Oreo Data Google Document: https://docs.google.com/spreadsheet/ccc?key=0Asfrwh-y1pyQdDJiT1c4YlNEcDBwMjJnWGlFUmx5c3c&usp=sharing#gid=0 Before I give my results for the data I analyzed I will explain beforehand how I found all of this information. For each data set I am finding the mean, median, mode, and range.
Mean:
To find the mean you need to add up all of the measurements in the data set and once you find the sum of all of the numbers you divide the number of measurements in your data set from the sum you just calculated.
For example, my data set is 3, 3, 4, 5, 6
Add up all of the numbers in the set so, 3+3+4+5+6= 21
Now since we have 5 numbers in this set we will divide 5 from 21. So 21/5= 4.2
So our mean or average is 4.2
Median:
The median is the number found in the middle of the set. I personally find the median by organizing the data in order from smallest to largest and then I cross off the smallest number and then the largest number, then I cross off the second smallest and then the second largest. I keep crossing off numbers until I get to the middle number.
For example, using the example data set I used before, 3, 3, 4, 5, 6
The median would be 4, because it is the middle number, so 3, 3, 4, 5, 6
Mode:
The mode is the number that appears the most in the data set so once again using the data set 3, 3, 4, 5, 6 the number that appears the most is the number 3. It is okay to have more than one mode.
Range:
The range shows the distance between the smallest and largest number in the set. To find the range you take the smallest number in the set and then subtract it from the largest number. So using 3, 3, 4, 5, 6 I would take 6-3=3. So the range from the smallest to the largest number is 3.
I first analyzed the data for the stuf in the Single Stuf Cookies. I started with the weight of the stuf.
Mean: 3.43 grams
Median: 3.3 grams
Mode: 3.0 grams and 3.5 grams
Range: 5 grams
I then analyzed the height for the stuf in the Single Stuf Oreo's.
Mean: 0.29 centimeters
Median: 0.30 centimeters
Mode: 0.30 centimeters
Range: 0.25 centimeters
Finally, I analyzed the the diameter of the stuf in the Single Stuf Oreo's.
Mean: 3.47 centimeters
Median: 3.50 centimeters
Mode: 3.50 centimeters
Range: 0.80 centimeters
Next, I analyzed the data for the stuf in the Double Stuf Oreo's. I started with the weight of the stuf.
Mean: 6.32 grams
Median: 6.30 grams
Mode: 5.80 grams
Range: 3.70 grams
Then I analyzed the height of the stuf.
Mean: 0.49 centimeters
Median: 0.50 centimeters
Mode: 0.50 centimeters
Range: 0.20 centimeters
Then I analyzed the diameter of the stuf in the Double Stuf Oreo's
Mean: 3.76 centimeters
Median: 3.70 centimeters
Mode: 3.70 centimeters
Range: 0.50 centimeters Now it's time to analyze the Mega Stuf data! Of course, I started with weight.
Mean: 9.39 grams
Median: 9.10 grams
Mode: 9.0 grams
Range: 3.50 grams
Then I looked at height.
Mean: 0.69 centimeters
Median: 0.70 centimeters
Mode: 0.80 centimeters
Range: 0.30 centimeters
And finally I looked at diameter of the stuf.
Mean: 4.17 centimeters
Median: 4.20 centimeters
Mode: 4.0 centimeters
Range: 0.60 centimeters
Reflection: Looking at all of this data it shows that the Double Stuf Oreo's have more stuf than the Single Stuf Oreo's and the Mega Stuf Oreo's have more stuf than the Double Stuf Oreo's. The thing is, there isn't much more stuf in each different type of cookie. According to the mean of the weight, height, and diameter of the Double Stuf Oreo it is about doubled the size to the Single Stuf Oreo. For the Mega Stuf there is only a little more stuf than in the Double Stuf, but the bottom line is there is in fact more stuf. Also, it really depends on the individual Oreo. Looking at the individual data some Oreo's varied in amount of stuf. Overall, this activity would be fun for children because we are applying math to cookies and what child doesn't love cookies?
Feedback: Are my explanations of mean, median, mode, and range clear? I had difficulty explaining and wording, specifically the median via blog. I feel if I had an actual class in front of me and a white board I could explain these better.
In class on Friday we spent the whole class period figuring out the components of our glyph design. We decided to make our glyph's Jack-O-Lantern's since it is October and close to Halloween. We decided as a class through voting and discussing what each feature of our pumpkin would represent. Such as, the grooves on the pumpkin represent how many siblings you have, or the color outline of the pumpkin represents your favorite color. For my daily work on Friday I created my own Jack-O-Lantern to share with the class on Monday. Here is an example of my finished Jack-O-Lantern glyph.
I really enjoyed this glyph activity so for my weekly work I decided to teach someone else what a glyph is and how to make one. I decided to use the codes and designs we already created in class to teach to someone else.
Since I went back home to Illinois this weekend to visit my family I had my one and only Mom help me out with my weekly work! I decided to explain to her everything we did in class on Friday and teach her how to make her own using our codes.
 First I explained to my Mom what a glyph was. I explained it as being a picture that contains data or information about someone. To make a glyph you create codes for the features of your picture. The codes represent data about you. Such as your favorite super power. The code we used in class was for the mouth of our pumpkin and whatever super power you liked the best you matched it up with the certain mouth. To the right is the code we used in class.
My mom caught on quickly on how to make a glyph and started creating her Jack-O-Lantern right away. This was her end result: Reflection: Overall I really enjoyed this activity and think that it would be an excellent activity for my future students. It think this activity would be a good beginning of the school year activity to get to know all of the students and have all of the students get to know each other. Also, I believe this activity lets kids be creative with creating codes and questions and designing their glyph. It's also great that each student's glyph will be unique.
Feedback: Was my explanation of a glyph clear?
In class on Friday we watched the show Cyberchase. I thought it was funny that we watched this show, because it brought me back to the 4th grade when my friend and I would watch Cyberchase and Arthur after school. So, this week I thought it would be fun to relive my childhood some more and watch another episode of Cyberchase since the main focus of the show is math. I also decided to play some online Cyberchase games located on the PBS Kids website! Since we started working on finding an area in class, I decided to watch the Cyberchase episode, "Sensible Flats". This episode link was located on our math course page under "Extra Resources" and led me to the Cyberchase page on the PBS Kids website. In the episode "Sensible Flats" the kids in the show had to help prove the villain character, Hacker, innocent. In the town the judge, Judge Trudy, claimed that everyone in the town had to have the same area of land as everyone else which was 15 square feet. Judge Trudy's land was in the shape of a rectangle so it was easy to tell what the area was, since to find the area of a rectangle you just have to multiply length by width, so in this instance, 5x3=15 square feet. Hacker's land was shaped differently, but still ended up having an area of 15 square feet. In the episode the kids proved that Hacker's shape had an area of 15 square feet by putting the shape on a graph/grid. This then demonstrated that his shape was made of squares and triangles. They showed that when you rearranged the squares and triangles, you end up with the same shape and hence the same area of 15 square feet. Here's a link to a video clip from the episode "Sensible Flats" showing how to find the area of a shape that is not a rectangle:
http://www.pbslearningmedia.org/resource/vtl07.math.measure.polg.regirregar/comparing-regular-and-irregular-areas/ 
This Cyberchase episode was great and it explained in a kid friendly way how to find the area of an odd shape that is not a rectangle.
Reflection: From this activity I realized some children's television really is educational and can help enhance children's understanding and learning of different subjects. I believe that television shows make learning fun and interesting for a child.This activity also made me realize how many different educational television shows there are such as, Sesame Street, Liberty's Kid, Arthur, and even Dora the Explorer. In my classroom I will definitely, occasionally use television for my lessons. Feedback: How much educational television would you allow your students to watch? Is there a such thing as too much educational television? Sources: http://pbskids.org/cyberchase/videos/All of my pictures are from a Google Image search
This week I really wanted to play a math game, and on the course page under extra resources I saw my professor posted "Quadrilaterals Connect Four". I love the original game of connect four and thought a math version of connect four would be fun.
In the directions it says two teams of two are needed to play the game successfully. Unfortunately the only person willing to play this exciting math game with me was once again my good friend, Tony. (He likes math, he's a math major) So, I did not see any harm in altering the game rules/directions a little bit and make it a two person game.
To prepare for the game I cut out two sets of the game cards, one set for me, and the other set for Tony. I colored one set of cards blue, for tony and the other set of cards orange, for me. 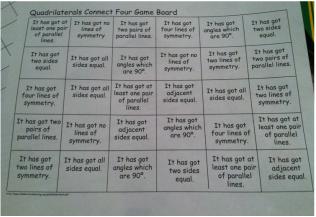 After getting the cards ready, I printed out the Connect Four game board. Each square has a description. Ex: "It has at least one pair of parallel lines"
After prepping for the game I explained the game rules to Tony. The game is exactly like connect four, but using quadrilaterals.
Each team should take their cards and place them face down. When it is their turn, they turn over the top card and place it where it belongs on the game board.
Ex: I pulled a rectangle from the card pile, the rectangle can go on the "I has angles which are 90 degrees" box.
The winner of the game gets four quadrilaterals in a row either diagonally, vertically, or horizontally.  Here is an example of a winning game board in which I won the game.
 Tony and I played several games in which he won some and I won some. It was a lot of fun and got a little competitive. Overall, I thought it was a great activity.
Reflection: I thought this was a great activity to help review the different quadrilaterals. I think this activity would be good for grades 3-5. I think it should be played when reviewing for an assessment, but I don't think it should be played when first learning the different quadrilaterals. The one bad thing about the game was the terrible grammar and sentence structure on the game board, I would definitely fix that as a teacher, because for some reason it bothered me immensely!Feedback: Were my directions clear? How could I change up the rules of the game to make the game better? Source: http://www.collaborativelearning.org/quadrilateralsc4.pdf
|






























 RSS Feed
RSS Feed